引言
在人类瞳孔的方寸之间,上演着自然界最精妙的模式识别奇迹:婴儿能在六个月辨认人脸,艺术家瞬间捕捉光影变化,这种与生俱来的视觉智慧,却让计算机科学家困扰了半个世纪——如何让冰冷硅晶理解纸墨间的温度?
从1943年McCulloch手绘的第一个神经元数学模型,到现代十亿百亿参数规模的Transformer巨兽,人工智能经历了一场堪比生命进化的认知革命。手写数字识别恰似这只”数字怪兽”的胚胎形态:784个像素点构成的混沌宇宙中,神经网络正通过矩阵变换与梯度流动,重走着人类文明从结绳记事到抽象符号的认知之路。
这不仅是技术演进的编年史,更是一场关于”如何教会机器看世界”的哲学探险。当28×28像素网格中跃动的数字被赋予意义,当交叉熵损失函数化作严师手中的教鞭,我们正在见证硅基文明突破图灵测试的全新可能——这一次,认知的火花不再局限于碳基生命的神经突触,而是在GPU的硅基躯体中星火燎原。
数字识别
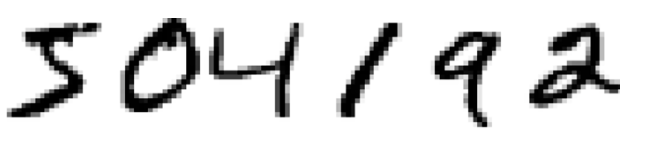
图 1-1
对于图1-1中的手写体数字,相信大家能识别出来,504192,在人类眼中不过是一瞥即解的简单任务。这看似轻松的认知过程背后,是亿万年进化塑造的精密视觉系统:从视网膜的感光细胞到大脑V1-V5视觉皮层的多级信息处理,构成了自然界最强大的模式识别引擎。
但当我们将这项任务交给计算机时,魔法的面纱瞬间揭开。传统的规则编程在此刻显得如此笨拙——试图用if-else语句穷尽所有书写变体,就像用算盘计算量子力学方程。正是这种认知鸿沟,催生了机器学习的革命性突破。

上面这段视频截图录制于 1993 年,主人公是图灵奖得主 Yann LeCun(杨立昆)。彼时 LeCun 才 32 岁,刚刚进入贝尔实验室工作,而视频里机器学习识别的第一段数字 201-949-4038,是 LeCun 在贝尔实验室里的电话号码。更为惊艳的是,视频比经典手写数字数据集 MNIST 的问世还要早 6 年。
目前通过机器学习,尤其是神经网络模型进行手写体识别,准确率已经能达到99%以上。
神经网络发展历程
- 早期阶段 (1940s – 1960s)
- 1943年:McCulloch 和 Pitts 提出了第一个形式化的神经网络模型——MP模型,这是神经网络理论的开端。
- 1958年:Frank Rosenblatt 提出了感知机(Perceptron),这是第一个能实际运行的单层神经网络,能够解决线性可分问题。
- 低谷期 (1970s – 1980s)
- 在这段时间里,由于计算能力有限以及理论上的挑战(如感知机无法解决非线性问题),神经网络的研究进入了低谷。
- 复兴与扩展 (1980s – 1990s)
- 反向传播算法(Backpropagation)的提出解决了多层神经网络的学习问题,这标志着深度学习时代的开始。
- 这个时期也出现了许多重要的架构,例如Hopfield网络、Boltzmann机等。
- 现代发展 (2000s – 至今)
- 随着计算能力的提升(尤其是GPU的出现),大规模数据集的可用性和更先进的优化算法,神经网络得到了飞速的发展。
- 卷积神经网络(CNNs)在图像处理领域取得了巨大成功。
- 循环神经网络(RNNs)和长短期记忆网络(LSTMs)在序列数据处理方面表现优异。
- 生成对抗网络(GANs)能够生成非常逼真的图像和其他类型的数据。
- Transformer架构革新了自然语言处理领域,推动了诸如BERT、GPT等预训练模型的发展。
现在,神经网络已经成为人工智能领域不可或缺的一部分,其应用范围涵盖了几乎所有需要自动化决策或模式识别的领域。
神经网络的基本组成
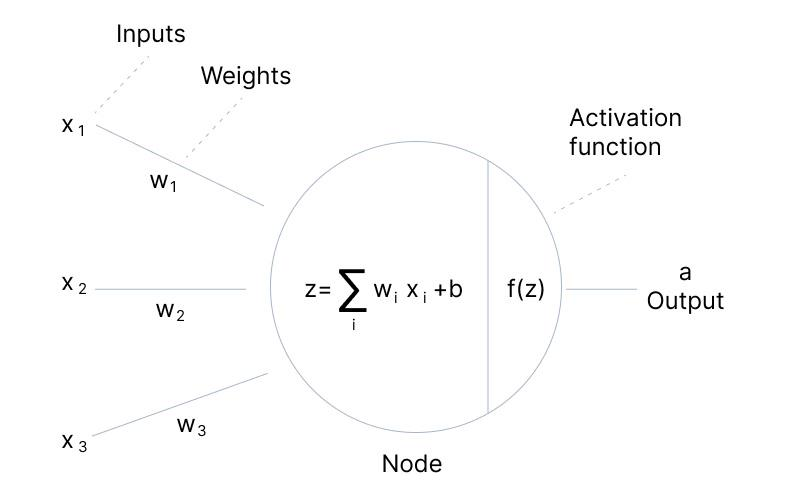
- 节点(Neuron Node):类似于大脑中的神经元,每个节点都有一个权重和一个阈值,用来决定何时激活。
- 层(Layer):神经网络由多层节点组成,包括输入层、隐藏层和输出层。输入层接收原始数据,输出层产生最终结果,而隐藏层则负责处理中间信息。
- 权重(Weight):连接节点之间的线有强度,这个强度就是权重,权重决定了信息传递的重要性。
- 激活函数(Activation Function):用于决定节点是否应该被激活,常见的激活函数有sigmoid函数、ReLU函数等。
一个简单的神经网络
只包含一个节点(神经元)的神经网络:
\(y=f(\sum_i w_i\cdot x_i)\)
把多个节点(神经元)连接起来,就构成了神经网络。神经网络之所以被称为网络,是因为它们通常用许多不同函数复合在一起来,构成链式结构来表示。
$$y=f(\sum_i w_i\cdot x_i)$$
$$z=f(\sum_i w’_i\cdot y_i)$$
$$\tau=f(\sum_i w”_i\cdot z_i$$
而对于最开始提到的手写体识别问题,其可能的神经网络可能如图1-2。
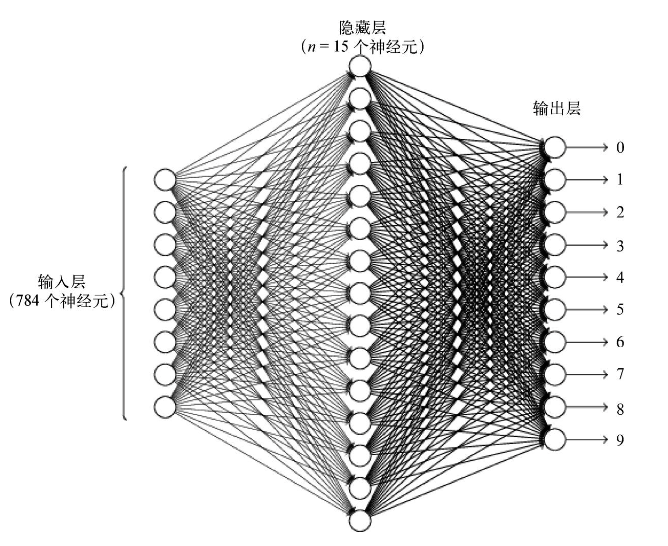
图1-2
输入层包含对输入像素的值进行编码的神经元,这里所用的训练数据由很多扫描得到的手写数字图像组成(像素是 28×28),因此输入层共包含 784(28×28)个神经元
隐藏层,包含 15 个神经元。
输出层,包含 10 个神经元。通过把输出神经元的输出以 0~9 编号,并计算哪个神经元的激活值最大,比如如果编号为 0的神经元被激活,那么说明神经网络猜测输入的数字为“0”,其他神经元的行为与之类似。
神经网络框架
device = "cuda" if torch.cuda.is_available() else "cpu"
'''
定义了名为 NeuralNetwork的类,该类继承自 torch.nn.Module。
在 PyTorch 中,所有的神经网络模型都应该从这个基类继承,
以便利用自动梯度计算和 GPU 支持等功能
'''
class NeuralNetwork(torch.nn.Module):
def __init__(self, num_inputs, num_outputs):
'''
构造函数(__init__)中定义了网络的层结构。
super().__init__() 调用初始化父类 nn.Module。
self.layers 是一个顺序容器,包含了一系列线性层和 ReLU 激活函数。
第一个线性层 nn.Linear(num_inputs, 30)
nn.ReLU() 是一个非线性激活函数,用于引入非线性特性到网络中。
第二个线性层 nn.Linear(30, 20) 将前一层的输出 30维映射到另一个20维 空间。
再次使用 nn.ReLU() 激活函数。
最后一个线性层 nn.Linear(20, num_outputs),
将20维向量映射到 num_outputs维输出。
'''
super().__init__()
self.layers = torch.nn.Sequential(
# 1st hidden layer
torch.nn.Linear(num_inputs, 30),
torch.nn.ReLU(),
# 2nd hidden layer
torch.nn.Linear(30, 20),
torch.nn.ReLU(),
# output layer
torch.nn.Linear(20, num_outputs),
)
def forward(self, x):
'''
forward 方法定义了数据通过网络的流动方式。当调用网络实例并传递输入 x时,会自动执行此方法。
logits = self.layers (x) 将展平后的向量传递给线性-ReLU 堆栈,
并返回最终的未归一化输出,通常称为 “logits”。
forward 方法是在 nn.Module 类中定义的一个特殊方法,它会被子类重写以定义网络的具体行为。在 PyTorch 中,所有自定义的神经网络模型都需要继承nn.Module 类,并且必须实现 forward 方法来描述数据如何通过网络的前向传播过程。
'''
logits = self.layers(x)
return logits
'''
定义模型对象,并打印。
输出结果为:
NeuralNetwork(
(layers): Sequential(
(0): Linear(in_features=50, out_features=30, bias=True)
(1): ReLU()
(2): Linear(in_features=30, out_features=20, bias=True)
(3): ReLU()
(4): Linear(in_features=20, out_features=3, bias=True)
)
)
'''
model = NeuralNetwork().to(device)
print(model)以上是一个简单的神经网络主体代码。
下面我们再回到手写体数字识别任务,深入了解下神经网络模型的工作机制。
手写体数字识别

手写体数字识别任务,就是从上述手写体图片中,通过神经网络模型,识别出正确的数字。
数据准备
PyTorch提供了特定领域的库,如TorchText、TorchVision和TorchAudio,它们都包括数据集。本例中,我们将使用TorchVision中的FashionMNIST数据集。
import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensor, Lambda, Compose
'''
下载 FashionMNIST 数据集,包括训练集和测试集
'''
training_data = datasets.FashionMNIST( root="data", train=True, download=True, transform=ToTensor(), )
test_data = datasets.FashionMNIST( root="data", train=False, download=True, transform=ToTensor(), )
'''
定义数据批次大小。
在神经网络中,“批次”(Batch)是指在训练过程中一次处理的数据集的一部分。批次的概念对于理解如何训练神经网络至关重要。
批次大小(Batch Size):指每个批次中包含的样本数量。例如,如果设置批次大小为 64,则每次训练迭代时,模型都会处理 64 个样本。
批次的作用
内存限制:由于计算资源有限,特别是当使用 GPU 训练大型神经网络时,一次处理整个数据集可能不可行。批次大小可以平衡内存使用和训练效率。
梯度更新:在每个批次上,模型计算损失并根据该批次的梯度更新参数。这样可以在每次迭代中获得关于模型性能的反馈,并相应地调整权重。
随机性:通过随机选择批次中的样本,可以引入一定程度的随机性,有助于模型学习更全面的特征表示。这种随机性有助于防止过拟合。
'''
batch_size = 64
'''
数据加载器 DataLoader 提供了许多有用的功能,比如:
自动分割数据集为批量数据。
支持异步数据加载和多进程数据加载,提高数据加载速度。
支持数据打乱,确保每个 epoch 中数据的顺序不同,有助于模型更好地学习。
'''
train_dataloader = DataLoader(training_data, batch_size=batch_size) test_dataloader = DataLoader(test_data, batch_size=batch_size)
'''
验证下训练数据的维度,
x.shape:torch.Size([64, 1, 28, 28]),分别对应批次大小、图片数量、图宽、图高。
y.shape: torch.Size([64]),对应同等批次大小的手写识别结果。
'''
for x,y in train_dataloader:
print(x.shape, y.shape)
想查看datasets都包含哪些数据集,可以执行
print(dir(datasets))
['CIFAR10', 'CIFAR100', 'CLEVRClassification', 'CREStereo', 'Caltech101', 'Caltech256', 'CarlaStereo', 'CelebA', 'Cityscapes', 'CocoCaptions', 'CocoDetection', 'Country211', 'DTD', 'DatasetFolder', 'EMNIST', 'ETH3DStereo', 'EuroSAT', 'FER2013', 'FGVCAircraft', 'FakeData', 'FallingThingsStereo', 'FashionMNIST', 'Flickr30k', 'Flickr8k', 'Flowers102', 'FlyingChairs', 'FlyingThings3D', 'Food101', 'GTSRB', 'HD1K', 'HMDB51', 'INaturalist', 'ImageFolder', 'ImageNet', 'Imagenette', 'InStereo2k', 'KMNIST', 'Kinetics', 'Kitti', 'Kitti2012Stereo', 'Kitti2015Stereo', 'KittiFlow', 'LFWPairs', 'LFWPeople', 'LSUN', 'LSUNClass', 'MNIST', 'Middlebury2014Stereo', 'MovingMNIST', 'Omniglot', 'OxfordIIITPet', 'PCAM', 'PhotoTour', 'Places365', 'QMNIST', 'RenderedSST2', 'SBDataset', 'SBU', 'SEMEION', 'STL10', 'SUN397', 'SVHN', 'SceneFlowStereo', 'Sintel', 'SintelStereo', 'StanfordCars', 'UCF101', 'USPS', 'VOCDetection', 'VOCSegmentation', 'VisionDataset', 'WIDERFace']构建神经网络单元
'''
self.flatten = nn.Flatten()
创建一个 Flatten 层,将输入的多维张量展平为一维向量,然后将其发送到全连接层中。
self.linear_relu_stack = nn.Sequential(...)
创建一个顺序容器 Sequential,用于堆叠多个层。定义神经网络的主体部分,包括多个线性层和激活函数。
nn.Linear(28*28, 512),
定义一个线性变换层,将输入的 28x28 图像展平后的 784 维向量映射到 512 维空间。
nn.ReLU(),
定义 ReLU 激活函数,为线性变换层的输出引入非线性特性。
nn.Linear(512, 512),
定义另一个线性变换层,将前面的 512 维向量再次映射到 512 维空间。
nn.ReLU(),
再次定义 ReLU 激活函数,为第二个线性变换层的输出引入非线性特性。
nn.Linear(512, 10)
定义最后一个线性变换层,将 512 维向量映射到 10 维空间,对应于 MNIST 数据集中的 10 个类别(数字 0 到 9)。
'''
class MinstNN(nn.Module):
def __init__(self):
super(MinstNN, self).__init__()
self.flatten = nn.Flatten()
self.layers = nn.Sequential(
nn.Linear(28*28, 512),
nn.ReLU(),
nn.Linear(512, 512),
nn.ReLU(),
nn.Linear(512, 10)
)
def forward(self, x):
x = self.flatten(x)
logits = self.layers(x)
return logits
'''
输出模型,结果为
NeuralNetwork(
(flatten): Flatten(start_dim=1, end_dim=-1)
(linear_relu_stack): Sequential(
(0): Linear(in_features=784, out_features=512, bias=True)
(1): ReLU()
(2): Linear(in_features=512, out_features=512, bias=True)
(3): ReLU()
(4): Linear(in_features=512, out_features=10, bias=True)
)
'''
model = MinstNN()
print(model)
值得注意的是,nn.Flatten() 层并不是在所有情况下都是必需的,但它在特定类型的网络架构中是非常有用的。在本例中,由于输入是 28×28 的灰度图像,而 nn.Linear 层期望一个一维张量作为输入,而28×28 的图像在经过展平后变成一个 784 维的向量,这样就可以适当地连接到后续的全连接层了。
训练模型
模型的训练,就是根据训练数据集x,找到一个逼近函数f,能更好的描述数据集的隐含特征,同时对新的数据集也能产生良好的预测行为。
损失函数
为了训练模型,我们需要定义一个损失函数(Loss Function)。损失函数在深度学习(机器学习)中扮演着非常重要的角色,它用于量化模型预测结果与实际结果之间的差异。简单来说,损失函数衡量的是模型的好坏,一个有效的模型应该能够最小化这个损失。
手写体识别任务本质上是一个分类问题,我们选择使用二元交叉熵损失函数 (Binary Cross-Entropy Loss)。
loss_fn = nn.CrossEntropyLoss() 优化器
我们还需要定义一个优化器。优化器(Optimizer)是用来更新神经网络权重(weights)和偏置(biases)的关键组件。其主要目的是最小化损失函数(loss function),从而使模型能够更好地拟合训练数据并做出准确预测。
本例中使用最简单的随机梯度下降(Stochastic Gradient Descent, SGD)算法,它是最简单的优化器之一,按照损失函数的负梯度方向更新权重。
'''
使用SGD优化器,并初始化学习率为1e-3
学习率(Learning Rate)是优化器中的一个重要超参数,它决定了模型参数(如权重和偏置)更新的速度。
学习率的作用包括:
1. 更新大小:学习率决定了每次迭代时权重更新的幅度。
2. 收敛速度:较高的学习率可以让模型更快地收敛,但可能会导致训练过程不稳定,甚至无法收敛。
3. 最小化损失:适当的学习率有助于找到损失函数的最小值。
'''
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3) 训练模型
device = "cuda" if torch.cuda.is_available() else "cpu"
'''
在训练周期内,模型使用训练数据集进行目标预测,并通过反向传播预测误差来调整模型的参数。
model.train() 设置模型为训练模式。
pred = model(X) 使用模型 model 对输入数据 X 进行前向传播,得到预测结果 pred。
loss = loss_fn(pred, y) 计算预测值 pred 和真实标签 y 之间的损失。
optimizer.zero_grad() 清除优化器中累积的梯度。这是因为优化器默认会累加梯度,这一步是为了避免梯度的重复累计。
loss.backward() 执行反向传播,计算损失函数关于所有可训练参数的梯度。
optimizer.step() 根据计算出的梯度更新模型的参数。这是通过优化器实现的,优化器会根据预设的学习率和其他配置来调整参数。
'''
def train(dataloader, model, loss_fn , optimizer):
model.train()
for batch,(X,y) in enumerate(dataloader):
X,y = X.to(device), y.to(device)
pred = model(X)
loss = loss_fn(pred, y)
optimizer.zero_grad()
loss.backward()
#print(w.grad)
#print(b.grad)
optimizer.step()
if batch %100 ==0:
loss = loss.item
print(f"loss: {loss:>7f}")模型评估
'''
model. eval();用来设置模型为评估(evaluation)模式。
with torch.no_grad(),上下文管理器用于禁用梯度计算,这可以减少内存消耗并加快推理速度,因为不需要保留计算图以备反向传播使用。
'''
def test(dataloader, model, loss_fn):
num_batches = len(dataloader)
size = len(dataloader.dataset)
model. eval();
test_loss , correct = 0, 0
with torch.no_grad():
for X, y in dataloader:
X, y = X.to(device), y.to(device)
pred = model(X)
test_loss += loss_fn(pred, y)
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
test_loss /= num_batches
correct /= size
print(f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")关于评估模式,这里简单解释下评估模式的主要作用:
- Dropout 层:
在训练模式下,dropout 层会随机关闭一部分神经元以防止过拟合。
在评估模式下,dropout 层不会关闭任何神经元,而是使用所有神经元的输出,同时将输出乘以 dropout 比例以模拟训练时的效果。
- Batch Normalization 层:
在训练模式下,batch normalization 层使用当前批次的统计信息(均值和方差)来标准化输入。
在评估模式下,batch normalization 层使用整个训练集的统计信息来进行标准化,这些统计信息是在训练过程中累积的。
何时使用评估模式:
验证/测试:在每个 epoch 结束时,通常会使用评估模式来评估模型在验证集或测试集上的性能。这样可以确保模型的表现不受训练时的随机性影响。
推理/部署:在模型部署到生产环境时,也需要使用评估模式,以确保模型的输出稳定且一致。
迭代
'''
训练loop--在训练数据集上迭代,试图收敛到最佳参数。
验证/测试loop--迭代测试数据集,以检查模型性能是否在提高。
'''
epochs = 100
for t in range(epochs):
print(f"Epoch {t+1}\n-------------------------------")
train(train_dataloader, model, loss_fn, optimizer)
test(test_dataloader, model, loss_fn)
print("Done!")以上就是整个模型的训练过程。
保存和加载模型
'''
保存和加载权重
'''
torch.save(model.state_dict(), 'model_weights.pth')
model.load_state_dict(torch.load('model_weights.pth'))
'''
保存和载入模型结构和权重
'''
torch.save(model, 'model.pth')
model = torch.load('model.pth')
模型导出为ONNX
ONNX(Open Neural Network Exchange)是一个开放的格式,用于表示机器学习模型。它允许不同框架之间的模型互操作性,使得模型可以在不同的框架中训练和推理。ONNX 的主要目标是提供一个统一的标准,使得开发者可以在不同的工具和平台之间无缝地迁移和使用模型。
import torch
import torch.onnx
onnx_filename = "model.onnx"
torch.onnx.export(
model,
dummy_input,
onnx_filename,
export_params=True, # 导出模型权重(非仅结构)
opset_version=14, # ONNX 算子集版本(推荐 ≥11)
do_constant_folding=True, # 优化常量计算(如固定形状的 reshape)
input_names=["input"], # 输入张量名称
output_names=["output"], # 输出张量名称
dynamic_axes={ # 动态维度(可选)
"input": {0: "batch_size"},
"output": {0: "batch_size"}
}
)综上,是一个典型神经网络模型工作全流程。所有的深度神经网络,都是基于简单的神经网络,通过增加不同网络层构建起来的,大语言模型的核心也是如此。
PyTorch 知识点
本章涉及到的 PyTorch 知识点:
torch.nn.Module
torch.nn.Module 是 PyTorch 中所有神经网络模型的基类,用于定义和管理神经网络的结构、参数及计算流程。
核心功能
参数管理:自动追踪所有子模块(nn.Module 对象)的参数(nn.Parameter)。
设备转移:通过 .to(device) 统一管理模型和参数的设备(CPU/GPU)。
序列化:支持通过 state_dict() 和 load_state_dict() 保存/加载模型状态。
计算图构建:通过 forward() 定义前向传播逻辑,自动构建反向计算图。
torch.nn.Sequential
torch.nn.Sequential是 PyTorch 中的一个容器模块,用于将多个层(或子模块)按顺序连接起来,形成一个复合模块。
核心功能
简化模型定义:对于简单的前馈神经网络,使用 Sequential 可以避免手动定义每一层之间的连接。
自动管理参数:所有嵌套在 Sequential 中的子模块参数会被自动管理和优化。
扩展和修改:通过添加、删除或替换 Sequential 中的子模块来快速调整模型结构。
torch.nn.Linear
torch.nn.Linear 是一个全连接层(Fully Connected Layer),也称为线性层。对输入数据执行线性变换,用于将输入映射到不同的特征空间。
torch.nn.ReLU
torch.nn.ReLU 是一个激活函数层,使用修正线性单元(Rectified Linear Unit)作为激活函数。非线性变换,将负值置为零,保持正值不变,用于深度学习模型中以引入非线性。
torch.nn.CrossEntropyLoss
torch.nn.CrossEntropyLoss 是一个用于多分类任务的损失函数。计算输入张量与目标类别之间的交叉熵损失。
torch.optim
torch.optim 是一个优化器模块,提供了多种优化算法来更新模型参数。根据损失函数的梯度信息,调整模型参数以最小化损失。